Fração é a representação da parte de um todo.
Para um inteiro dividido, possa ser considerado fração, a divisão entre todas as partes devem ser iguais, ou seja, todas as partes tem que ter o mesmo tamanho.
Em um número fracionário, o número de baixo sempre será o denominados, aquele que dá nome, que quantifica o todo e a parte de cima sempre será o numerador, aquele que numera, quantificando assim a parte a ser representada.
Assim, podemos concluir que o surgimento do número fracionário veio da necessidade de representar quantidades menores que inteiros, por exemplo, 1 bolo é um inteiro, mas se comermos um pedaço, qual seria a representação numérica que esse pedaço e o resto do bolo representaria? Foi a necessidade de criar uma representação numérica para as partes de um inteiro que proporcionou o surgimento dos números fracionários que iremos estudar nesta seção.
.
Tipos de Fração:
- própria: o numerador é menor que o denominador. Ex.:

- imprópria: o numerador é maior ou igual ao denominador. Ex.:

- mista: constituída por uma parte inteira e uma fracionária.
Ex.:  Pode-se encontrar uma fração imprópria a partir do número misto:
Pode-se encontrar uma fração imprópria a partir do número misto: 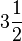 => 2x3= 6; 6+1= 7
=> 2x3= 6; 6+1= 7
 Pode-se encontrar uma fração imprópria a partir do número misto:
Pode-se encontrar uma fração imprópria a partir do número misto: 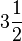 => 2x3= 6; 6+1= 7
=> 2x3= 6; 6+1= 7
(7=numerador/2=denominador), e assim por diante, repetindo o denominador
- aparente: é quando o numerador é múltiplo ao denominador, ou seja um número inteiro escrito em forma de fração. Ex.:
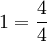
- equivalentes: aquelas que mantêm a mesma proporção de outra fração. Ex.:
 ou
ou  Veja que as frações se relacionam por um fator multiplicativo: no primeiro caso,
Veja que as frações se relacionam por um fator multiplicativo: no primeiro caso,  é 2 vezes
é 2 vezes  e no segundo caso
e no segundo caso 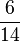 é 2 vezes
é 2 vezes 
- irredutível: o numerador e o denominador são primos entre si, não permitindo simplificações. Ex.:

- unitária: o numerador é igual a 1 e o denominador é um inteiro positivo. Ex.:

Operações com frações:
Adição e Subtração
A adição e a subtração de frações são feitas utilizando mínimo múltiplo comum, ou MMC.
Ex.: 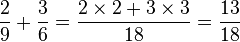 (O MMC de 9 e 6 é 18)
(O MMC de 9 e 6 é 18)
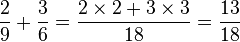 (O MMC de 9 e 6 é 18)
(O MMC de 9 e 6 é 18)Multiplicação
A multiplicação é efetuada apenas multiplicando-se os numeradores entre si e os denominadores entre si. Ex.: 

Divisão
Para efetuar a divisão entre duas frações, multiplica-se a fração que está no numerador pelo inverso da fração que está no denominador. Ex.:

No último passo foi feita uma simplificação de Frações.
Simplificação de frações:
Uma fração pode ser simplificada quando numerador e denominador não são primos entre si. Ex.:

Para tanto basta dividi-los pelo máximo divisor comum (MDC) entre eles, obtendo-se uma fração que, além de manter a proporção da original, é do tipo irredutível: 


Nenhum comentário:
Postar um comentário